Musings of an Analyst

Years ago, my first boss after I finished graduate school shared his beliefs that “all learning applies to everything else” and that “more brains are better for every job.”  I learned more from him than I have probably learned from any of my subsequent bosses.  Maybe that was him.  Maybe that is because of where I was then and where I have been since.

For today, my snarky take on this topic is the similarity between some responses of dynamic systems and the behavior of people or groups in a work environment.  For today, I was going to muse on three types of oscillators:

1. A lightly damped pendulum,
2. A circular path centrifugal pendulum vibration absorber, and
3. A Van der Pol Oscillator.

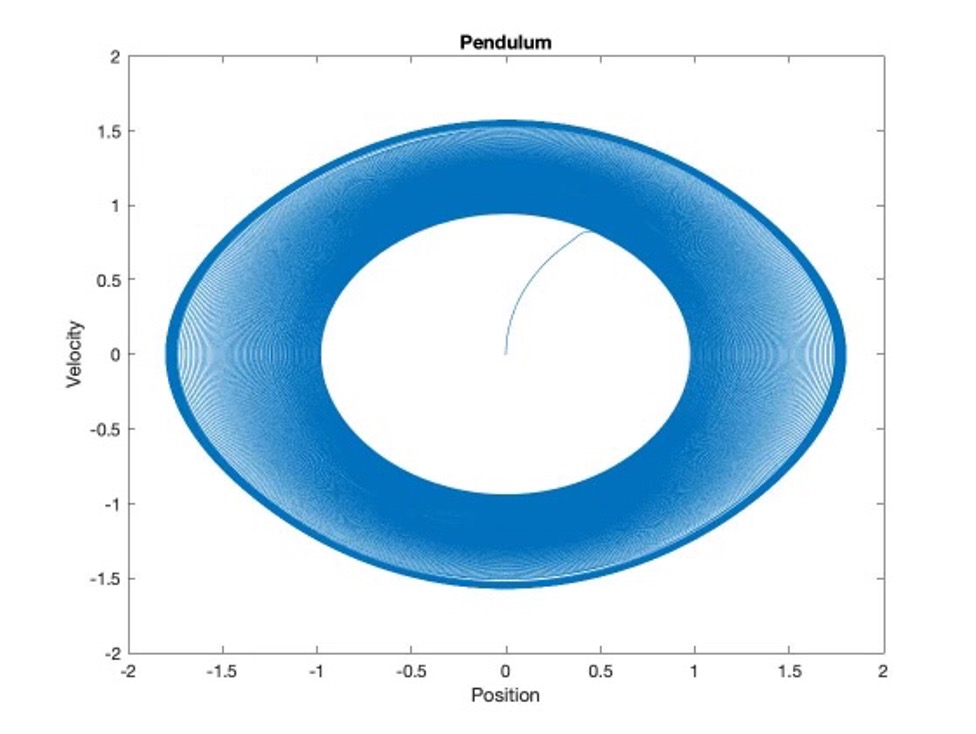
A lightly damped pendulum is just like the pendulum in a grandfather clock.  For this discussion, a ball on the end of a string may be an even better example as a starting point.  This a simple linear oscillator.  The lightly damped description simply means that it loses energy very slowly from things like friction, air resistance, etc.  When sufficiently perturbed from a resting state, the system (whether it be the ball on the end of the string, the discussion in a group, or an individual) goes around-and-around-and around-and-around.  It takes a very LOOOOONGGG time for this a system like this to stop going around in circles.  It take an even LOOOOONNNNNNGGGGER time for the system to settle down to a rest state or an “equilibrium” condition.  In the snarky but true category, many groups and individuals look a lot like this system.  On the plus side, this enables them to be responsive to inputs.  On the down-side, not a lot of positives to going around-and-around-and-around…

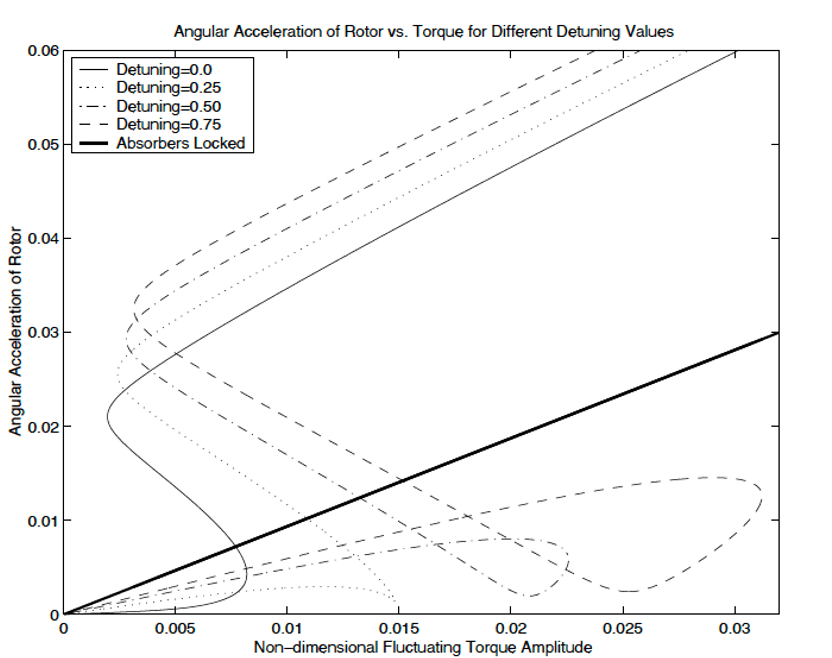
A lot of my academic work and early career work was focused on why stuff shakes and figuring out ways to make stuff not shake.  One of the types of systems that I got the opportunity to study and use was a class of systems called a centrifugal pendulum vibration absorber or CPVA.  For those inclined, the classic book by Den Hartog (https://a.co/d/fWAg647) has a good description of these devices.  Simplistically, these devices can be thought of as balls on the ends of strings.  The ball is attached to one end of the string and the other end of the string is attached to a rotor. The absorber can be tuned to absorb vibrational energy at a multiple of the rate that the rotor is spinning by tuning the ratio of the length of the string to the distance between where the string is attached and the center of the rotor.   If the rotor is spinning at 1000 RPMs, the absorber can be tuned to absorb energy at three times, four times, or x times the rate the rotor is spinning.  This attribute was what made these systems so useful for some of the airplane engines that were used in World War II.

For this discussion, I like the circular path version because it has dynamics that are particularly interesting and that result in an amusing (for me) analogy.  In this system, as the input energy is increased, the oscillator absorb and absorbs until a “bifurcation point” is reached.  At that point, the oscillator “jumps” to a different behavioral regime and transitions from absorbing input energy to amplifying input energy.  Once the oscillator has jumped, it continues to amplify input energy even if smaller amounts of energy are being input.  This amplifying behavior continues until a second “bifurcation” occurs at a lower amplitude input.  For me, it is hard to unsee the potential for this exact behavior in groups and individuals.

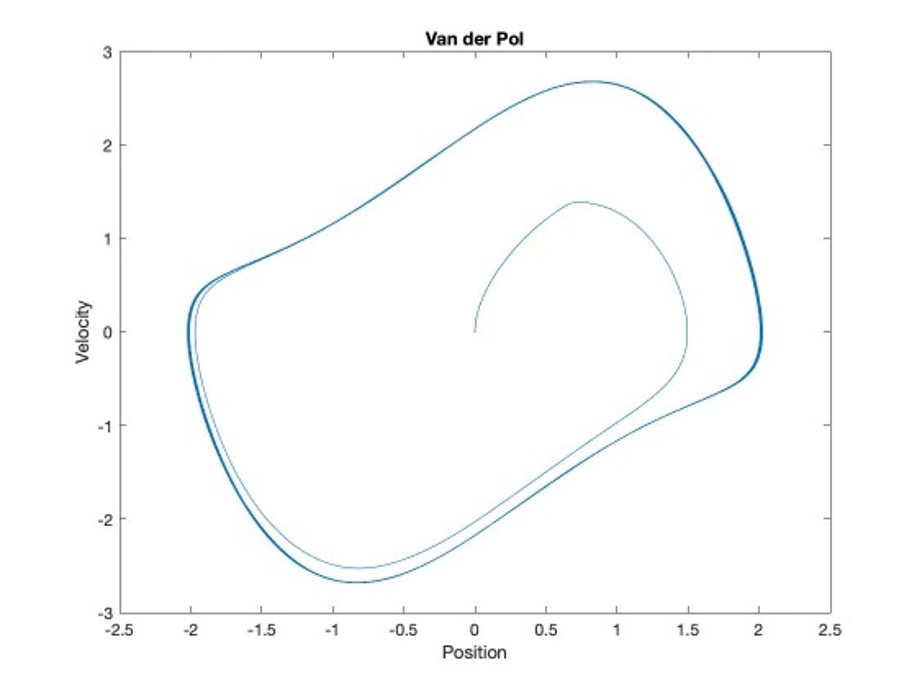
The last example I wanted to talk about today was a Van der Pol Oscillator.  This is a nonlinear oscillator which means that the dynamics are “richer” and more complicated than some of the more basic systems.  This system is such that once it is perturbed from a rest state, it spirals out to a stable dynamic orbit.  Once in this stable dynamic orbit, the system continues to oscillate and does not return to the rest condition.  In this stable dynamic state, the amplitude (or size) of the oscillation is independent of the initial perturbation.  If the initial perturbation was small, the oscillator can have a big stable response.  If the initial perturbation was big, this oscillator has the same big response.  Just like the other two oscillators mentioned above, it is hard not to see where individuals and groups can have behavioral patterns that are much like this oscillator.